|
Vectors are especially useful, because they can specify both direction and distance at the same time. |
||
VectorsOf primariy importance to analytic geometry is the concept of a vector. In mathematics, a vector is simply an ordered set of values. Vectors are represented in a similar fashion to points; that is, \((x, y)\) or \((x, y, z)\). Because of the possibility of confusion between the two, it is common practice to specify a vector using a right-pointing arrow above any variable or other designator to denote that it represents a vector. We also try to chose variables and symbols that are commonly used for vectors and make it clear that it is a vector. For example, if we might write a statement such as \(v=(x, y, z)\), in which case we can safely assume v represents a vector; but the same cannot be said if we were to write \(p=(x, y, z)\), because \(p\) is more commonly used to represent a point. In such cases where we want (or need to) use a representation from which we cannot derive such an assumption, we use the arrow notation: \(\overrightarrow{p}=(x, y, z)\), or if we really want, we can specify it long-hand as: vector \(p=(x, y, z)\). Vectors are one of the simplest forms of a line in mathematics. Just as with points and vectors, it may also be possible to confuse a line and a vector when specified by two points. Because of this, we again make our usage clear by either specifying it outright or by using the arrow notation (or both). For example, we might write \(\overrightarrow{PQ}\) to differentiate a vector from the line \(PQ\). Similarly, when drawing out a diagram, vectors are represented by arrows. There are two types of vectors: unit vectors and scalar vectors. A unit vector always has a length of 1 and is specified by a set of cosines. A scalar vector may have any length and not only specifies direction, but also magnitude. The concept of "north" would be specified by a unit vector, while "10 miles north" would be specified by a scalar vector. If k is a scalar and v is a vector, then kv is a vector whose length is |k||v| and whose direction is the same as or opposite to the direction of v, according to the sign of k. It is called a scalar multiple of v. Note that when we refer to something being a scalar or a scalar quantity, we really mean any single value that specifies scale. It is also important to note that in the representation |k||v|, |k| is the absolute value of k, and |v| is the vector length of v. 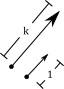
Vector Length
The length of a vector (also called its magnitude) can easily be determined by the Pythagorean distance equation \(d=\sqrt{a^2+b^2}\)
(2-space) or \(d=\sqrt{a^2+b^2+c^2}\) (3-space). This can be generalized to any number of dimensions (n-space) by the following equation:
Basis VectorsOf special interest are the unit vectors along the axes. In a plane, if the origin O=(0,0), X=(0,1), and Y=(1,0), then the vectors represented by \(\overrightarrow{OX}\) and \(\overrightarrow{OY}\) are denoted i and j, respectively, and are called basis vectors. Every vector in a plane can be written in the form ai+bj. The values a and b are called the components of the vector. In 3-space, vectors are written as ai+bj+ck. 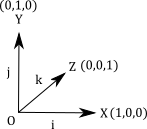
Direction Angles, Direction Cosines, and Direction NumbersGiven a unit vector in 3-space, \(\{α,β,γ\}\) is the set of direction angles, where \(α\) is the angle between v and i, \(β\) is the angle between v and j, and \(γ\) is the angle between v and k. Direction angles are never negative and are never greater than 180°. The direction cosines \(\{l,m,n\}\) for the vector are: \(l=cos\,α, m=cos\,β\), \(n=cos\,γ\). 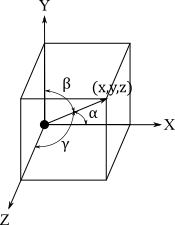
Given a vector length \(p\), where \(p=\sqrt{x^2+y^2+z^2} \), the direction cosines are: \(l=cos\,α=\)\(x\over p\), \(m=cos\,β=\)\(y\over p\), \(n=cos\,γ=\)\(z\over p\).
If there is a constant \(k\) such that \(a=kl, b=km, c=kn\), then \(\{a,b,c\}\) is the set of direction numbers for \(v\). We then get:
Normalizing VectorsIf we form the scalar multiple of the nozero vector \(v\) and the scalar \(1\over|v|\), the result is a unit vector in the direction of \(v\). This process is usually written as \(v\over|v|\), and is commonly refered to as "normalizing" a vector. Perpendicular VectorsLet's say that for some reason, we have a planar vector, and we need to determine a vector that is 90° to the right. This is quite simple. Given a vector v=ai+bj, its opposite is -ai-bj, and bi-aj and -bi+aj are both perpendicular. We can see by the figure below that bi-aj is to the right (clockwise) from ai+bj. 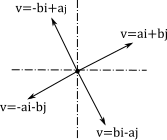
Vector Dot Product
The vector dot product, also known as a scalar product or inner product, has the effect (among other things) of comparing the directions of two
vectors. If the vectors are facing similar angles (less than 90° relative variation), the result is positive; opposing angles yeild a
negative result; and if the angles are perpendicular, the result is zero.
Dot Product (2-D)Similar to standard vector form, the dot product formula is generally written as: \(u\cdot v=a_1 a_2 + b_1 b_2\), where \(a\) and \(b\) are the components of the vectors. It would be clearer written as \(u\cdot v=u_x v_x + u_y v_y\), but this isn't the standard form.
It should be noted that \(u\cdot v=|u||v|\, cos\,θ\); that is, the dot product is the vector length of \(u\) times the vector length of
\(v\) times the cosine of their relative difference angle. We therefore write:
If both \(u\) and \(v\) are unit vectors, the denominator \(|u||v|\) is unity and can be omitted. The value \(\frac{1}{|u||v|}\) is a normalizing factor that is not needed if both u and v are unit vectors. Dot Product (3-D)
Spacial dot products are defined similarly to that of planar dot products, the main difference being the addition of a third dimension.
As with 2-D dot products, the denominator can be omitted if both \(u\) and \(v\) are unit vectors. Vector Cross ProductThe cross product, also known as a vector product, has the effect of producing a vector which is perpendicular to both \(u\) and \(v\). As we will later find, however this is not its only purpose. Due to the functionality of the cross product, it is ony defined for spacial (3-D) vectors. 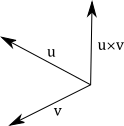
If \(u=a_1 i+b_1 j+c_1 k \) and \(v=a_2 i+b_2 j+c_2 k\), then the cross product is:
It is important to note that the order of the vectors matters. If the vectors are swapped, the result will point in the opposite
direction; that is:
The magnitude of the vector resulting from a cross product of two vectors is proportional to the sine of
the angle between the vectors. This can be seen in the following equation:
While there is no such thing as a cross product in two dimensions, a similar equation can be used to calculate the sine of the angle between two planar vectors, as is shown in the following matrix:
Algebraicly, the equation is:
Area of a TriangleGiven three vertices that represent a triangle, we could use the distance equation to calculate the lengths of each edge, then use Heron's formula to calculate the area; but we can skip all that and do it much faster. It is actually quite simple to determine the area of the triangle using vectors. 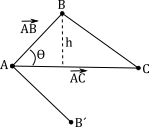
Given the diagram here, and with a little knowledge of trigonometry, we can see that the height \(h\) of the triangle can be calculated as:
|
||
| Analytic Geometry: Line Intersection | Analytic Geometry: Planes |